This article explains the reason why can't extend C drive on Windows 10 (32 & 64 bit) and what to do if unable to extend partition C by shrinking D or other volumes.
Why can't extend C drive in Windows 10
Many Windows 10 computer users encountered the problem that C drive is getting full, but nobody likes to reinstall Operating System and all programs. Luckily, Microsoft provides native Disk Management with Shrink Volume and Extend Volume to resize disk partition without losing data.
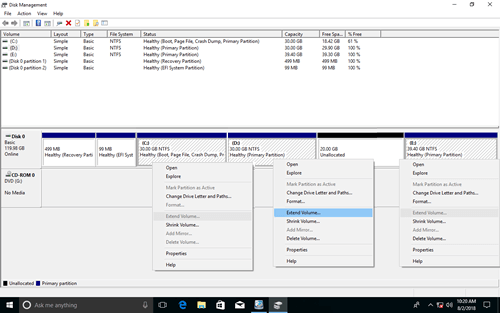
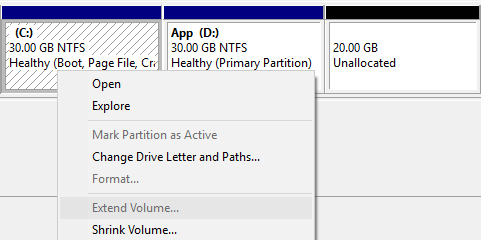
However, many people feedback that they can't extend C drive with Windows 10 Disk Management tool, because Extend Volume is disabled for C drive after shrinking D.
Yes, this is because both Shrink and Extend Volume functionality have serious limitations:
Shrink Volume cannot produce Unallocated space on either side. For example: when shrinking partition D, you can only enter an amount, and then it will produce Unallocated space on the right side for you.
Extend Volume can only extend a partition by merging the contiguous Unallocated space on the right side. So Extend Volume is always disabled, except you delete the right contiguous partition instead of shrinking.
As you see, Extend Volume is unable to extend drive C and E after shrinking D.
Do not delete drive D to enable Extend Volume for C drive, otherwise, many programs stop working even if you transfer all files in D to other partition.
In this situation, you need to move Unallocated space from right side of D to the left. I'll show you how to do this in next paragraph.
Let's see other reasons that cause unable to extend C drive in Windows 10 Disk Management.
Logical and Primary partition in MBR style disk
In Windows desktop and laptop, there are two style of disk: MBR and GPT. Because of many advantages of GPT style, many Windows 10 computers format disk as GPT by default.
To check disk style, press Windows and X on key board to open Disk Management, right click this disk and select Properties, then switch to Volume tab on the top.
Unlike GPT disk that create all partitions as Primary in it, MBR disk can only create maximum 4 Primary partitions, or 3 Primary plus 1 Extended partition. All Logical partitions must be created in the Extended partition.
As I said above, you can delete partition D to get contiguous Unallocated space (though not suggested), then Extend Volume will be enabled for C drive, but if partition D is a Logical partition, you still cannot extend C drive via Windows 10 Disk Management after deleting D.
In MBR disk, Unallocated space deleted from Primary partition cannot be extended to Logical partition, Unallocated deleted from Logical partition can't be extended to any Primary partition.
Another limitation: only NTFS and RAW partitions can be extended, however, this is not an issue to system C drive.
What to do if unable to expand C drive in Windows 10
Actually, it is very easy to solve this problem no matter which reason listed above.
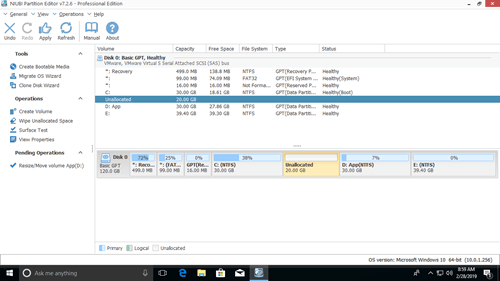
Firstly, let's see the solution of can't extend C drive after shrinking D in Windows 10 Disk Management. Download and install NIUBI Partition Editor.
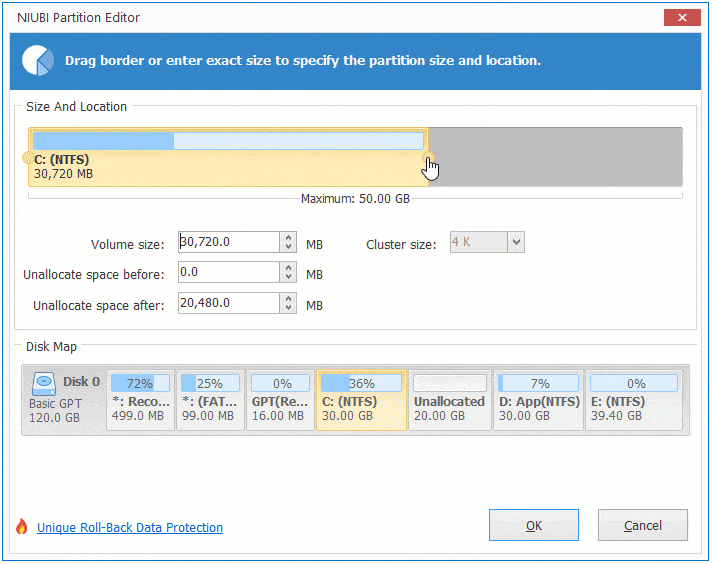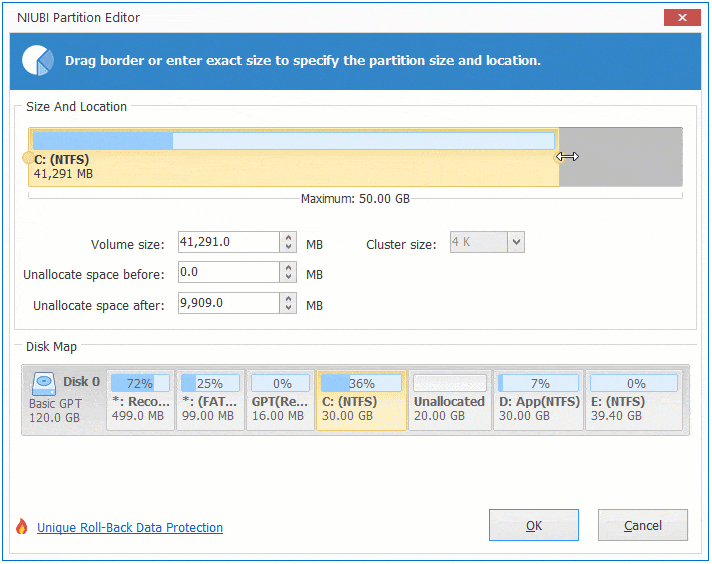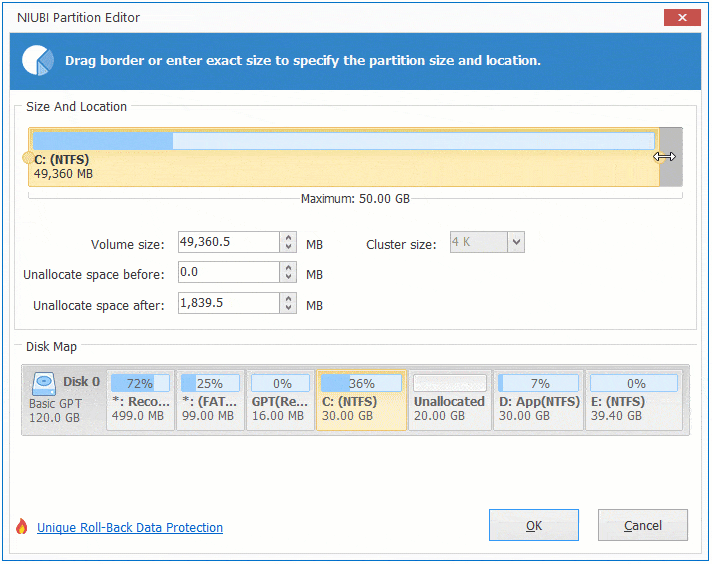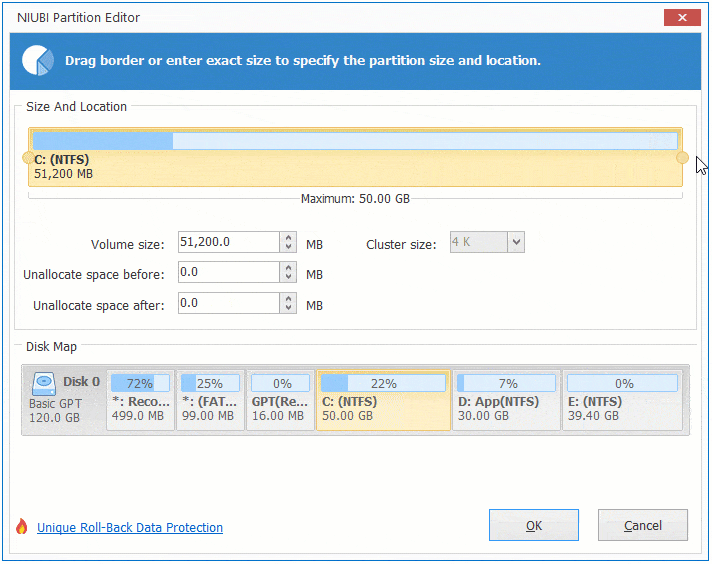
Step:1 Right click drive D and select "Resize/Move Volume", drag middle position rightwards in the pop-up window.
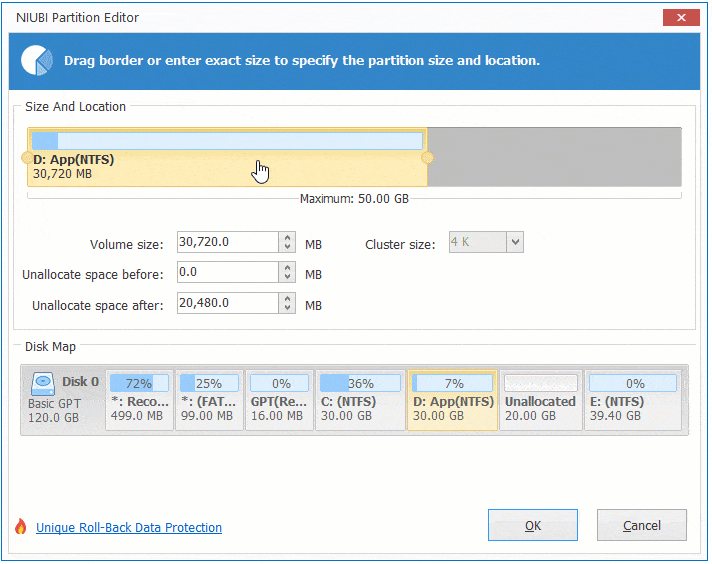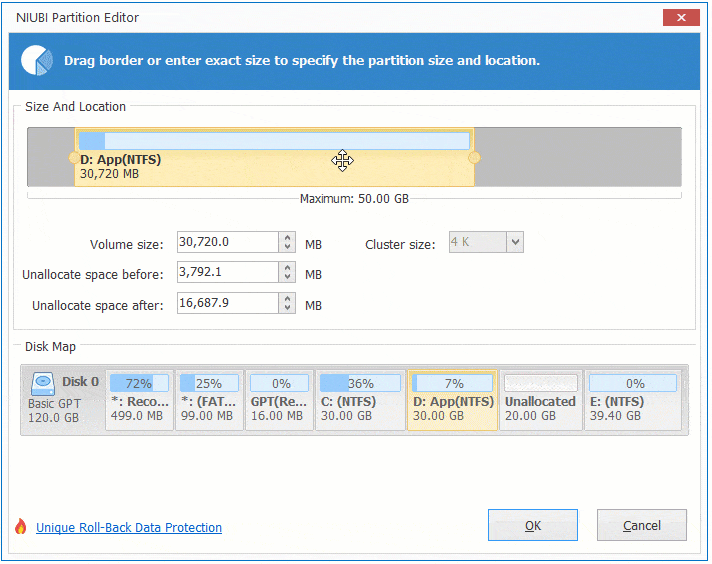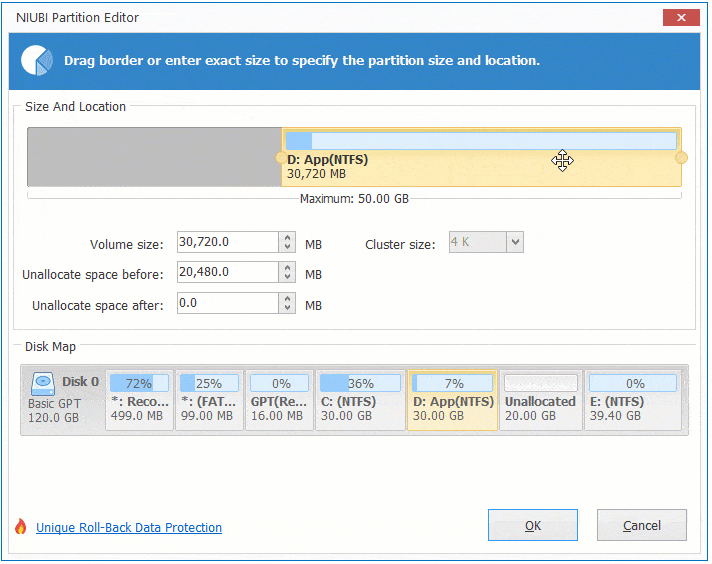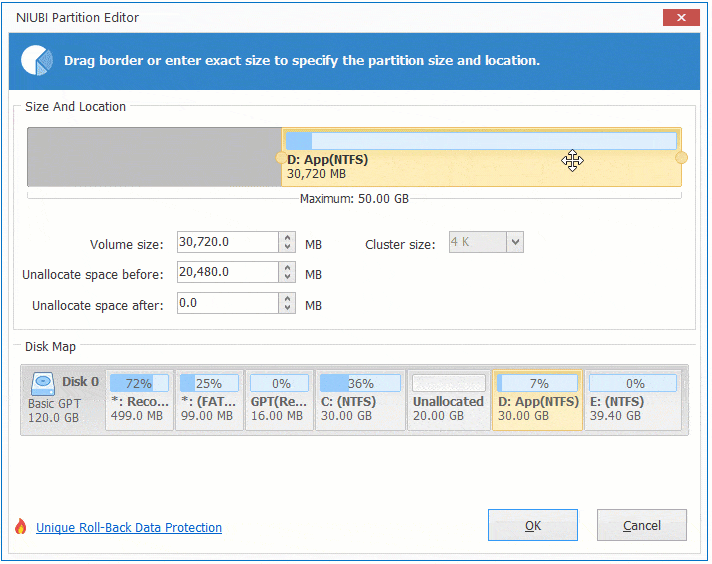
Then Unallocated space is moved to the left side of volume D.
Disk space of a Logical partition will be shown as Free after deleting in Disk Management, but NIUBI will show as Unallocated. If D is a Logical partition that causes can't expand C drive in Windows 10 after deleting, simply follow Step 2 above.
Special solution to extend partition C
Few computer has only no data volumes (only C and system reserved partition), the methods above is invalid in that case. Because all partitioning software cannot extend C drive to another separated disk.
Run "Disk Clone Wizard" feature to copy this disk to another larger one, and then you can extend C drive with the extra disk space.
In Summary
Windows 10 built-in Disk Management can't extend volume C by shrinking D, or by deleting D if it is Logical partition. As the safest and fastest tool, NIUBI Partition Editor can help you solve this problem easily, it also helps you do many other disk partition operations.